
Armando F. da Rocha1,2,3, Aline Lourenço1, Andrea G. Rondó3, Cecília S. Bursztyn1,3, Samanta Palmieri3, Renée X. Menezes2
1 - Núcleo de Estudos da Aprendizagem e Cognição, CAAD UNICID
2 - Lim 01 HC FMUSP
3 - EINA Estudos em Inteligência Natural e Artificial
E-MAIL: eina@enscer.com.br
RESUMO
É uma tradição de nossa cultura considerar a matemática como um sistema de processamento simbólico, que caracteriza e distingue, assim como a linguagem, o homem dos animais. Essa tradição associa a aritmética e a linguagem, e justifica a idéia de que o aprendizado e o uso dos números é dependente da capacidade de falar humana. Todo o ensino da aritmética organiza-se em torno da fala: o recitar dos números, a memorização das tabuadas como listas de frases, etc. Uma nova visão do problema apareceu incentivada pelo desenvolvimento das neurociências, na qual o conhecimento e o uso dos números é um processo resultante da evolução da vida na terra e suportado por circuitos neurais específicos. Esse conhecimento modifica a prática de ensino na sala de aula. Neste trabalho, apresenta-se resultados de uma pesquisa com crianças matriculadas da primeira à quarta séries do ensino fundamental, da rede pública, sobre a cronometria e as estratégicas de solução do cálculo aritmético. Discute-se os achados e propõ-se um modelo neural para o processo de contar a resolução da soma, subtração e multiplicação.
INTRODUÇÃO
É uma tradição de nossa cultura considerar a matemática como um sistema de processamento simbólico, que caracteriza e distingue, assim como a linguagem, o homem dos animais (Dehaene, 1991, Fayol, 1996). Platão considerava que os números tinham uma realidade própria, que o homem poderia descobrir através da razão. Pitágoras defendia proposição semelhante, e criou uma escola que defendia a primazia do número como forma de pensamento puro.
Essa tradição associa a aritmética e a linguagem, e justifica a idéia de que o aprendizado e o uso dos números é dependente da capacidade humana de falar. Todo o ensino da aritmética organiza-se em torno da fala: o recitar dos números, a memorização das tabuadas como listas de frases, etc.
Uma nova visão do problema apareceu incentivada pelo desenvolvimento das neurociências, na qual o conhecimento e o uso dos números é um processo resultante da evolução da vida na terra e suportado por circuitos neurais específicos (Ashcraft, 1991; Butterworth, B., 1999; Dehaene, 1991, Fayol, 1996, Gallistel and Gelman, 1991; Winn, 2000). Dentro dessa nova proposição, a capacidade de quantificação e de manipulação e cálculo de quantidades, é uma necessidade evolutiva, pois o animal para sobreviver tem que sempre avaliar onde tem mais alimento e menos inimigos.
Dentro dessa nova visão, os circuitos neurais para quantificação surgem precocemente na escala evolutiva e são aprimorados gradativamente até atingir a complexidade dos processos de cálculo humano. Descobre-se, então que animais contam (Butterworth, B., 1999; Dehaene, 1991, Dehane, 1997; Galistel and Gelman, 1991) e que o bebê humano calcula ( Winn, 2000). O cérebro que calcula é independente do cérebro que fala, embora os dois conjuntos de circuitos neurais partilhem inúmeras relações (p.e., Butterworth, B., 1999, Mix, 1999).
As neurociências descobrem que o processo de contagem é um processo de controle visuo-motor e não verbal, complexo e que é distinto para números pequenos (até 4 ou 5) e para números maiores (acima de 7) (Galistel and Gelman, 1991; Gelman and Meck, 1983; Fayol, 1991; Fink et al, 2001; Jensen et al, 1950; Kaufmann et al, 1949; Mix, 1999; Sathian et al, 1999). As quantidades pequenas são percebidas em bloco, rapidamente, enquanto que o reconhecimento de quantidades maiores depende de um processo serial de observação. A contagem em bloco é rápida e o tempo de reconhecimento das quantidades é praticamente constante entre 1 a 4. A contagem serial depende da focagem seqüencial do olho sobre os objetos a contar, e portanto o tempo para o reconhecimento da quantidade contada é dependente do número de objetos, e portanto do tamanho do número contado (p.e., Galistel and Gelman, 1991; Fink, et al, 2001; Fayol, 1991; Mix, 1999). A contagem por blocos de sons é explicada pela análise de ritmos - o números de eventos sonoros é derivado da freqüência com que os eventos sonoros são percebidos, enquanto que a contagem serial de sons dependeria de um processo interno de representação não verbal de eventos (p.e., Mix, 1999).
A dissociação entre os circuitos neurais para linguagem e matemática impõe que os processos de cálculo aritmético tenham que ser modelados sem o recurso de regras codificadas lingüisticamente as famosas tabuadas. Essa proposta contrasta violentamente com toda a tradição secular de que a aprendizagem dos fatos aritméticos é dependente da habilidade verbal da criança (p.e., Dehaene et al, 1999) e exige que os processos didáticos se modifiquem para explorar as habilidade visuo-motoras das crianças.
Estudos sistematizados realizados com diversos grupos de crianças em distintos países do mundo tem mostrado que as crianças utilizam múltiplas estratégias para solucionar os problemas aritméticos propostos (Butterworth, 1999; Dehaene, 1991, Dehane, 1997; Siegler, 1996). Assim, por exemplo, o processo de adição (Fig. 1) pode ser resolvido com as seguintes estratégias (Dehane, 1997; Rocha, 1999; Siegler, 1996):

Fig. 1- As estratégias de solução da adição
Tem-se mostrado que o tempo que a criança ou o adulto leva para solucionar um problema de adição, é proporcional ao tamanho dos números envolvidos na operação (p.e., Ashcraft, 1991; Butterworth, 1999, Dehaene, 1991, 1997, Fayol, 1996, Groen and Parkman, 1972; McCloskey, 1991). Os resultados experimentais obtidos parecem indicar que várias estratégias podem estar sendo utilizadas na solução, pois mostram boas correlações entre o tempo de resposta e a raiz quadrada da soma ou produto dos operando ou mesmo com o valor do menor desses operandos. Resultados semelhantes tem sido obtidos para a subtração (p.e., Fayol, 1991; Dehaene, 1997, Wood et al, 1975). Entre as estratégias utilizadas para solução da subtração podem ser citadas as contagem decrescentes se a diferença entre os operando é pequena, ou crescente se essa diferença é grande (p.e., Butterworth, 1999, Dehaene, 1997, Fayol, 1996).
Os resultados acima indicam que o processo de memorização verbal dos fatos aritméticos (Dehaene, 1997) não deve ser a estratégia utilizada para suportar o processo de cálculo mental, mas parecem indicar que as operações mentais devem ser suportadas pela internalização e otimização dos processo de manipulação ou contagem numérica. Essa internalização dependeria do aprimoramento de circuitos neurais filogeneticamente herdados para identificação e operação com quantidades de objetos observados.
Outra vez, os achados das neurociências sobre os processos mentais de cálculo entram em conflito com a didática suportada pela tradição cultural, de um processo simbólico apoiado na capacidade lingüística humana.
As técnicas recentes de mapeamento da atividade cerebral por ressonância magnética funcional (fRMI), tomografia por emissão positrônica (PET-scan), magneto e eletroencefalografia tem sido utilizadas para identificação dos circuitos neurais para cálculo mental (refs). Esses achados têm mostrado que diferentes áreas corticais e subcorticais participam dos circuítos envolvidos nos processamentos da soma, adição, subtração e multiplicação, quer sejam exigidos resultados precisos ou aproximados. Tem sido proposta uma participação importante de áreas temporo-parietais nos processos de quantificação numérica; de circuitos frontoparietais na comparação e ordenação de números; de neurônios de áreas de linguagem na compreensão de problemas apresentados oralmente e para verbalização de resultados, mas de neurônios visuais quando as tarefas são apresentadas visualmente.
Rocha e colaboradores (Foz et al, 1999. Rocha, 1999, Rocha et al, 2000, Rocha e Rocha, 2001) desenvolveram uma metodologia de mapeamento cerebral que permite a investigação da atividade cerebral durante a realização de tarefas cognitivas apresentadas através de video-jogos. Os resultados têm mostrado que é possível com essa metodologia relacionar a atividade cerebral e a performance associadas a esses jogos com o desenvolvimento escolar (vide Rocha et al, nesse número); caracterizar a evolução do processamento cerebral da linguagem com a idade; identificar a plasticidade dos circuitos neurais de linguagem em caso de lesões cerebrais congênitas, etc.
Em virtude da inexistência de dados sobre os processos de cálculo mental utilizados por crianças brasileiras para solução de operações aritméticas, e da ausência de dados na literatura internacional sobre o mapeamento da atividade cerebral nessas condições, decidiu-se investigar esses processos em um grupo de crianças cursando o Ensino Fundamental. O presente trabalho relata os resultados obtidos entre o tempo de resposta e o tamanho dos operandos.
METODOLOGIA
Um grupo de 27 crianças cursando o Ensino Fundamental, na rede pública da cidade de São Paulo, participaram do presente estudo. Essas crianças foram recrutadas como voluntárias entre aquelas que freqüentam o serviço de Odontopediatria, Faculdade de Odontologia, UNICID.
Essas crianças foram submetidas a uma bateria de jogos com a finalidade de identificar o seu desenvolvimento cognitivo e escolar. A avaliação foi realizada em dois dias não consecutivos: no primeiro deles estudou-se a competência em leitura e escrita e a segunda sessão foi dedicada a avaliação da aritmética. As atividades utilizadas para esses fins são aquelas definidas no software "Aprendendo com Juca e Laura" para avaliação cognitiva. Os resultados nessas atividades foram utilizados para classificar as crianças como aptas a freqüentar uma das quatro séries do Ensino Fundamental, de acordo com os programas curriculares especificados por Rocha e Rocha, 2001. De acordo com essa classificação, as crianças foram distribuídas nos seguintes grupos:
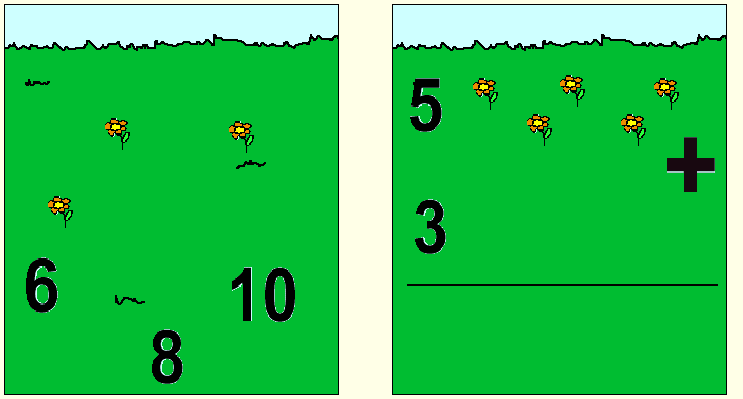
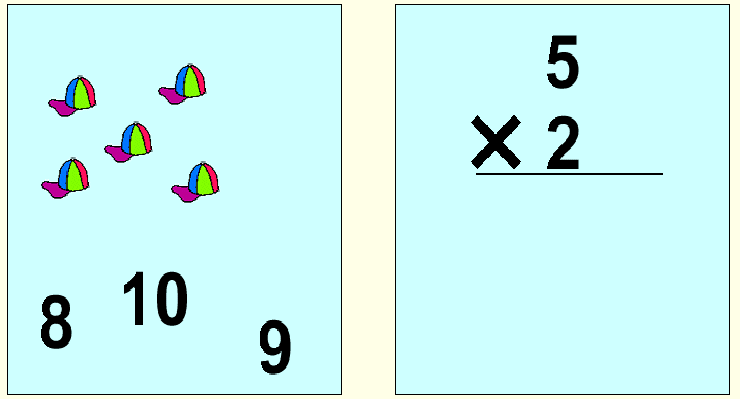
Fig. 2 Exemplos de atividades de soma e multiplicação
Veja texto para maiores explicações
Essas classificações apresentaram um correlação de cerca de 80% com a atual série cursada pela criança.
As crianças voltaram ao laboratório do Núcleo de Estudos da Aprendizagem e Cognição (NEAC), CAAD, UNICID, para realização de um conjunto de atividades de leitura, escrita e aritmética semelhantes àquelas utilizadas na avaliação cognitiva enquanto o seu eletroencefalograma (EEG) era registrado de acordo com o sistema 10/20. Nessa sessão o tempo de resposta foi registrado pelo próprio software "Aprendendo com Juca e Laura" e associado ao correspondente registro de EEG. Os resultados que aqui serão descritos correspondem às atividades de aritmética. Aqueles correspondentes às atividades de linguagem serão relatados em outra oportunidade.
Exemplos de atividades utilizadas para estudo dos processos de cálculo aritmético são mostrados na Fig. 2, para o caso da adição e produto. A conta a ser realizada é apresentada visualmente, no formato habitualmente utilizado em sala de aula. Concomitantemente, no caso da soma e subtração, o número de objetos correspondente ao maior operando é apresentado ao seu lado, enquanto que o número de objetos correspondente ao menor deles é mostrado em outro quadro à esquerda da operação à realizar. No caso da multiplicação, apresentava-se nesse quadro o número de objetos correspondente ao maior multiplicando, enquanto que para a divisão mostrava-se os objetos associáveis ao divisor. A criança tinha a possibilidade de manusear os objetos apresentados dentro de qualquer uma das estratégias de cálculo discutidas na literatura (p.e., Butterworth, 1999; Dehaene, 1991, Dehane, 1997; Siegler, 1996), ou poderia optar pelo cálculo mental. Um conjunto de 3 números eram mostrados para que um deles fosse escolhido como o resultado da operação proposta.
| 5 + 3 |
3 2 |
| 5 + 4 |
7 4 |
| 6 + 5 |
4 2 |
| 4 + 2 |
9 3 |
| 3 + 2 |
5 2 |
| 6+ 3 |
8 5 |
| soma |
subtração |
| 6 x 2 |
4 / 2 |
| 4 x 4 |
8 / 2 |
| 3 x 2 |
9 / 3 |
| 5 x 3 |
12/ 4 |
| 5 x 2 |
20 / 4 |
| 3 x 3 |
12 /3 |
| produto |
divisão |
Tabela I Os cálculos aritméticos realizados
Cada criança realizou seis cálculos de cada uma das operações aritméticas (Tab. I), envolvendo apenas operadores de um dígito no caso da soma, subtração e produto, e divisores e resultados de um dígito no caso da divisão.
O tempo decorrido desde a apresentação do jogo até a tomada de decisão sobre o resultado da operação foi obtido a partir dos tempos marcados de cada evento, para cada um dos cálculos propostos para cada operação. Tabelas associando esses tempos de respostas (TR) e os números envolvidos em cada um dos cálculos foram montadas para cada operação aritmética, para permitir o estudo de regressão entre TR e os operandos n1, n2 de cada operação. Realizou-se os cálculos estatísticos para as relações entre TR e: n1, n2, raiz quadrada de ( n1+ n2), raiz quadrada de ( n1* n2) e ( n1- n2). Esses cálculos foram processados apenas para os dados obtidos com aquelas crianças que não utilizaram nenhuma manipulação dos objetos disponibilizados pelo jogo, isto é, as regressões foram calculadas apenas para os casos em que não houve uma manipulação ostensiva dos elementos de cálculo. Entretanto, observou-se que muitas vezes as crianças utilizaram movimentação de dedos ou olho que indicavam um processo de contagem aberta. Essas observações predominaram no caso da soma, sendo raras no caso da subtração e praticamente inexistentes para o produto e divisão. O critério de exclusão utilizado acima, reduziu drasticamente o número de observações no caso da divisão, o que inviabilizou o estudo estatístico dos resultados obtidos para essa operação.
Um dos experimentadores observou as crianças durante todo o período de realização das tarefas, com o objetivo de determinar o tipo de estratégia utilizada pela criança na solução das operações aritméticas. Específicamente, o experimentador anotava qualquer movimentação de dedos ou olhos associada ao processo de contagem de elementos das operações; qualquer contagem oral ou qualquer outro comentário emitido pela criança. Registrava também qualquer tipo de erro cometido na solução da tarefa e o número de tentativas para obter essa solução.
RESULTADOS
A tabela II mostra a distribuição por grupo e operação, do número e porcentagem de crianças que efetuaram os diferentes cálculos solicitados, sem utilizar a manipulação dos objetos disponíveis nas atividades utilizadas.
Observa-se que apenas cerca de 50% do total das crianças foram capazes de resolver a soma e a subtração sem o auxílio da manipulação explícita acima descrita, embora muitas delas tenham realizado manipulações discretas tais como, movimentação ocular e/ou de dedos, contagem oral, etc. - durante a realização do "cálculo mental" utilizado para obter o resultado da operação. Deve-se salientar que a manipulação discreta foi mais reduzida para a subtração do que para a soma. Quando considerados os grupos, verifica-se que a soma e subtração foram realizadas por 62% crianças do grupo A e, respectivamente, por 36 e 43% dos indivíduos do grupo B.
O produto e a divisão foram solucionadas apenas pelas crianças do grupo B. Nenhuma das crianças do grupo A se declararam capazes de realizar essas operações, e quando testadas, não conseguiram solucionar esses tipos de cálculo. O produto foi solucionado por cerca de 73% das crianças do grupo B e a divisão por cerca de 40% desses indivíduos. Deve-se ressaltar que o uso da manipulação discreta foi extremamente reduzida no caso das operações de produto e divisão.
O número de erros cometidos pelas crianças incluídas na tabela II foi extremamente baixo, em geral, menor que 2% dos cálculos realizados para as operações de soma e subtração, e também não diferiu estatisticamente entre os grupos ou entre essas operações. O número de erros na solução do produto foi também baixo (menor que 2%) para as 11 crianças incluídas na tabela II e muito alto (maior que 60%) para os 3 indivíduos restantes do grupo B. Esse fato, determinou a exclusão desses indivíduos da análise estatística do tempo de solução da tarefa. A taxa de erro maior foi encontrada para a divisão, pois 8 dos 14 indivíduos do grupo B cometeram mais de 60% de erros na solução da operação, tendo sido, por esse motivo, excluídos da tabela II. O restante dos indivíduos desse grupo realizaram todos os cálculos corretamente.
O tempo médio para solução de cada um dos tipos de operação pelas crianças incluídas na tabela II, foi de 7,5 segundos para a soma; 5,3 segundos para a subtração; 4,1 segundos para o produto e 5,9 para a divisão. O tempo de resposta do produto foi estatisticamente diferente daquele para a soma e subtração. Os tempos de resposta para a soma e subtração também diferiram estatisticamente. O tempo de resposta para a divisão não mostrou nenhuma diferença estatística em relação às outras operações, devido ao pequeno número de observações para esse tipo de cálculo.
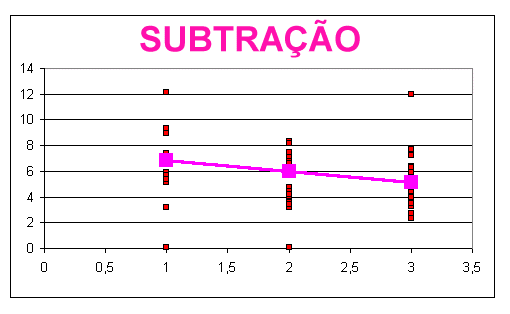
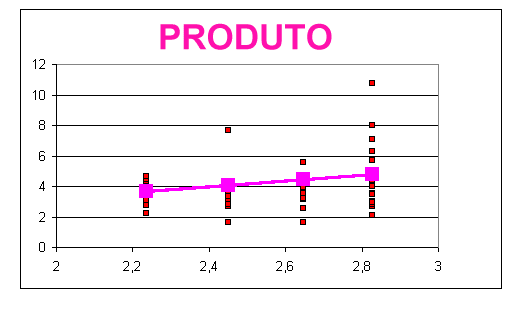
Os resultados da análise estatística do tempo de resposta em relação ao tamanho dos operandos, são mostrados na figura 2. O tempo de solução da soma mostrou-se uma função linear crescente da raiz quadrada da soma dos operandos. O coeficiente de correlação para essa função foi de 25%, com uma significância estatística de p < 2%. Função semelhante foi encontrada para o caso do produto, cujo coeficiente de correlação foi de 26%, com significância estatística de p < 4%.
A subtração diferiu das operações de produto e soma, pois o tempo de solução dessa operação foi função linear decrescente do mínimo entre o subtraendo n2 e do resultado r. O coeficiente de regressão para essa relação foi de 29%, com significância estatística de p < 5%.
| OPERAÇÃO |
TOTAL |
GRUPO A |
GRUPO B |
|||
| N |
% |
N |
% |
N |
% |
|
| SOMA |
13 |
48 |
8 |
62 |
5 |
36 |
| SUBTRAÇÃO |
14 |
52 |
8 |
62 |
6 |
43 |
| PRODUTO |
11 |
41 |
0 |
0 |
11 |
73 |
| DIVISÃO |
6 |
22 |
0 |
0 |
6 |
40 |
Tabela II Os cálculos aritméticos realizados

| a |
b |
função |
R |
p |
m |
operação |
| -3,8 |
4,04 |
Ö n1 + n2 |
.27 |
.02 |
7,5 |
soma |
| 7,7 |
-.86 |
Min( n2, r ) |
.29 |
.02 |
5,3 |
subtração |
| -.9 |
1,87 |
Ö n1 + n2 |
.26 |
.04 |
4,1 |
produto |
Fig. 3 Relação entre tempo de resposta e tamanho dos operandos
a - coeficiente linear; b coeficiente angular; R coeficiente de correlação, p significância estatística; m tempo médio
DISCUSSÃO
As neurociências têm mostrado que os processos de contar e calcular são suportados por circuitos neurais semelhantes, e distintos daqueles envolvidos na produção e compreensão da linguagem. O contar começa a ser entendido como um processo de coordenação motora dos atos de localizar e apontar ou marcar os objetos de interesse, e um processo neural de quantificação dos objetos assim identificados (e.g., Dehane et al, 1998; Jahanshahi et al, 2000, Mix, 1999; Ratinckx et al, 2001; Rickard et al, 2000; Rocha e Rocha, 2001, Win, 1998).
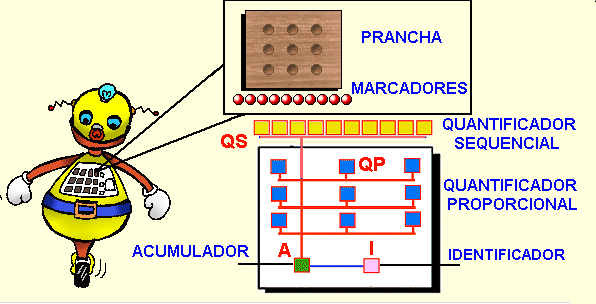
Fig. 4 Um modelo de quantificador
Um mecanismo básico para o processo de contagem foi proposto por Meck and Church, 1983, baseado em um acumulador, cujo nível de ativação define os objetos já contados. O modelo da Fig. 4 utiliza essa idéia para propor um circuito básico para o processo de contagem e cálculo que incorpora os principais achados da literatura e servirá para explicar os resultados do presente trabalho.
Nesse modelo, um identificador I um circuito neural visual, auditivo, tátil, etc. identifica o objeto a ser contado. A cada identificação, o elemento I envia um pulso para o acumulador A que muda seu nível de atividade (Fig. 5 Operando por unidade). Esse acumulador A, que pode ser constituído por um ou mais neurônios, está conectado a um conjunto de outros neurônios que serão chamados de quantificadores. Define-se dois grupos desses elementos: os quantificadores proporcionais e os sequenciais (fig. 4), que podem, por exemplo, controlar as marcas na prancha do robô, mostrando a quantificação realizada.
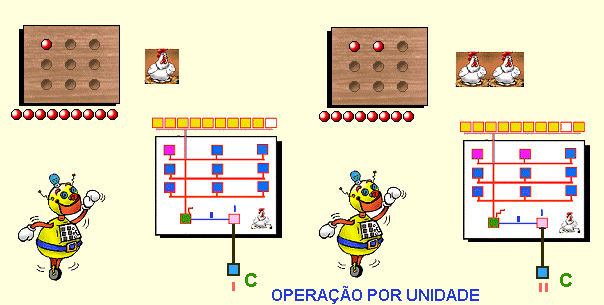
Fig. 5 Operando com unidades
O nível de atividade do acumulador A poderá excitar os quantificadores proporcionais QP dependendo de seus limiares de ativação. Esse limiar deve crescer ordenadamente, por exemplo de 1 a 9 e da esquerda para a direita e de cima para abaixo (Figs. 4 e 5), de modo que número de QPs excitados é diretamente proporcional à ativação do acumulador A, pois toda vez a atividade a de A for maior que o limiar Li de QPi, isto a > Li, esse quantificador será ativado.
A ativação dos quantificadores sequenciais QS obedece a uma regra diferente. Cada quantificador QSi tem dois limiares de ativação:
a) o limiar inferior Lii que define a mínima quantidade de atividade de A necessária para ativar QSi ,
b) o limiar superior Lsi que define a máxima quantidade de atividade de A que pode ativar QSi .
Desse modo, QSi só será excitado se a atividade a de A for maior que Lii e menor que Lsi, isto é se Lii < a < Lsi. Os diversos QS devem ser ordenados espacialmente de acordo com seus limiares, por exemplos aqueles de menor limiares devem ficar à direita daqueles de maiores limiares (Fig. 4 e 5).
No processo de contar, o robô localiza e aponta um objeto de interesse. Quando isso ocorre, o identificador I aumenta a atividade de A em uma unidade, que por sua vez determina a ativação de um número proporcional de QP e um dos QS (fig. 5). Esse processo de contagem será chamado aqui de Contagem por Unidade.
As neurociências tem mostrado também que os humanos e os animais são capazes de contar rapidamente pequenas coleções ( 1 a 4 ) de objetos, no processo chamado de Contagem por Bloco (e.g., Fink et al, 2001; Mix, 1999, Sathian et al, 1999). O modelo da Fig. 4 pode ser facilmente adaptado para esse tipo de processamento, bastando para isso, assumir que o identificador I poderá reconhecer e quantificar essas pequenas coleções, de modo que o número de pulsos ( por exemplo, 2 na Fig. 6 ) que enviará para o acumulador A dependerá do número de elementos identificados por bloco.
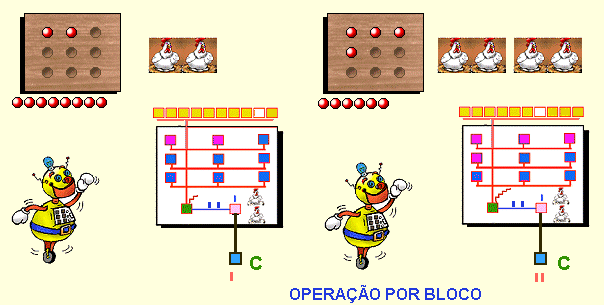
Fig. 6 Operando com blocos
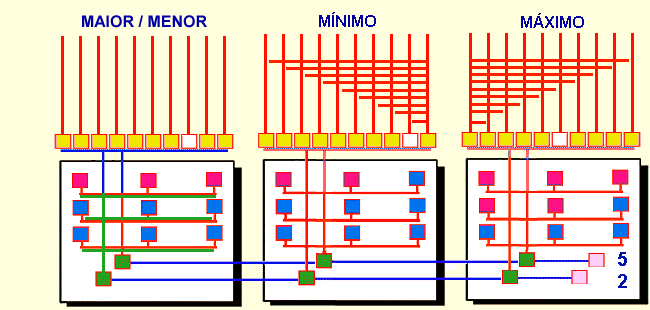
Fig. 7 Comparando quantidades
O circuito básico da Fig. 4 pode ser modificado para outros usos, como por exemplo, comparar quantidades (Fig. 7), bastando para isso, que circuitos distintos de identificadores I e acumuladores A sejam conectados adequadamente aos QPs e QSs.
Permitindo-se que os QSs possam inibir a atividades de outros QSs (Fig. 7), pode-se criar circuitos para identificação do mínimo se a inibição for ordenada da direita para a esquerda, ou do máximo se a ordenação for no sentido oposto (Rocha, 1992). Permitindo-se que o acumulador A com menor ativação iniba os QSs enquanto que o acumulador A com maior ativação excite esses QSs, o números desses quantificadores ativados dependerá da diferença de atividade nos dois circuitos. Esse tipo de circuito (Fig. 7) indicará quando uma quantidade é maior ou menor que a outra. A comutação entre excitação e inibição no circuito Maior/Menor definido na Fig. 7, pode-se determinada pelos circuitos Máximo/Mínimo.
Os circuitos definidos nas Figs. 4 a 7 mostram que vários tipos de processamento com quantidades podem ser realizados sem qualquer referência à linguagem humana, e ressaltam que o processo de contar depende fundamentalmente da habilidade de localizar e identificar os objetos de interesse. No caso humano isso implica, principalmente, na otimização dos controles da movimentação ocular (localização e identificação) e da mão (apontar ou marcar). O processo de contar pode ser acelerado, toda vez que for possível identificar pequenos blocos de objetos. Esse é o processo de contagem por múltiplos.
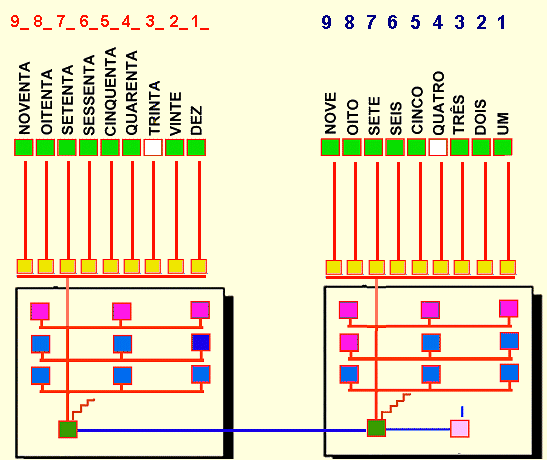
Fig. 8 Codificando quantidades
Os circuitos mostrados nas Figs. 4 a 6 são capazes também de suportar as relações entre aritmética e linguagem, para isso basta que seja possível um mapeamento dos QSs com os neurônios de controle da fonação para números na área de Broca ou daqueles para reconhecimento das formas visuais dos números arábicos talvez localizados no giro angular (fig. 8). Dessa maneira estaria garantida a codificação das quantidades reconhecidas por esses circuitos tanto na fala quanto na leitura e escrita. Da mesma maneira, pode-se imaginar o mapeamento de neurônios sensoriais que reconheceriam os sons e as imagens dos números, diretamente sobre os respectivos QSs.
Nessa proposta, a relação entre linguagem e aritmética desenvolve-se paralelamente em decorrência da otimização dos circuitos neurais para linguagem e aritmética, determinados pela aprendizagem que deve ser independente, porém associada. Por independente se quer ressaltar que a aprendizagem do contar e calcular não é subordinada ao aprender do falar, ler e escrever, como é tradição em nossa cultura. Por associada se quer ressaltar que o aprendizado concomitante e coerente facilitará o mapeamento entre os QSs e os neurônios dos circuitos neurais para linguagem, quer oral, visual ou escrita.
Os processos de cálculo aritmético podem ser vistos agora como um simples processo de contagem serial no caso da soma e subtração, ou por bloco principalmente no caso do produto e divisão.
No caso das estratégias de manipulação global e simplificada, a proposta acima decorre do simples fato de que a criança conta os elementos dos conjuntos que representam os cálculos a serem realizados. No caso do chamado cálculo mental, pode-se imaginar um mecanismo cerebral para simulação da contagem, que simule as ações utilizadas nas estratégias mais primitivas, do mesmo modo que a rotação mental ajusta a posição de imagens visuais através de um processamento neural, sem a necessidade da movimentação real da cabeça. Esses circuitos para simulação da Contagem por Unidade ou por Bloco podem ser facilmente criados adicionando-se um (circuito) controlador ou contador C do identificador I, que internamente simule o processo de localizar e identificar os objetos que representam os operandos do cálculo aritmético. Esse controlador C (Fig. 5 e 6) acionará o identificador I da mesma maneira com que os objetos reais guiam os processos motores oculares e manuais de sua localização e marcação.
Os resultados do presente trabalho podem ser interpretados dentro da hipótese de que os processos de cálculo aritmético são suportados por sistemas neurais semelhantes àqueles utilizados no processo de contar, como proposto inicialmente na literatura (Groen e Parkman, 1972). Além disso, pode-se propor que o indivíduo poderá utilizar diferentes estratégias de cálculo (como aquelas discutidas por Siegler, 1996), suportada por circuitos neurais distintos, na solução de uma mesma operação.
Assim, pode-se sugerir que os resultados obtidos aqui para a cronometria da soma, sejam explicados pela solução dessa operação a partir de um circuito de contagem, no qual os operandos são sucessivamente incrementados no acumulador A, numa simulação dos processos de contar semelhantes àqueles mostrados na figura 1, de acordo com a estratégia utilizada.
A simulação da chamada manipulação total, implica em que o processo de contar (números em preto na Fig. 1) é utilizado tanto na identificador dos numerais ( 3 e 4 na Fig. 1) que codificam os operandos quanto no processo de adição (números em vermelho na Fig. 1). Assim, primeiro seria contado 1,2 e 3 para identificação do operando 3; depois seria contado 1, 2, 3 e 4 para o operando 4, e finalmente, contado 1, 2, 3, 4, 5, 6 e 7 para obtenção do resultado. Essas simulações seriam organizadas pelo controlado C na fig. 5.
No caso da manipulação simplificada, poderia se admitir que a contagem seria restrita a obtenção do resultado, pois o reconhecimento dos numerais se faria por projeção direta de neurônios visuais com quantificadores seqüenciais de circuitos de representação numérica (Fig. 8) localizados em regiões temporoparietais (Dehane et al, 1998).
A regra do mínimo pode ser implementada assumindo-se que os operandos são inicialmente comparados, o máximo deles identificado por bloco e carregado em um só passo no acumulador A, enquanto que o menor dos operandos é seqüencialmente acumulado em A à partir da ação do controlador C (fig. 5). Finalmente, o chamado cálculo mental poderia ser assumido como resultado de uma contagem em bloco para os dois operandos.
Dentro da proposição acima, o tempo de resposta TR para a solução da soma deve ser uma função do tamanho dos números, pelo menos no caso das manipulações global e simplificadas e do tamanho do menor operando no caso da regra do mínimo. No caso do cálculo mental por bloco, esse tempo tenderia a ser mais constante. O fato do coeficiente de correlação (Fig. 3) para a relação TR = -3,8 + 4,04 raiz quadrada de ( n1 + n2) ter sido menor do que aqueles relatados na literatura (Butterworth, 1999; Dehane, 1997; Fayol, 1996) poderia ser explicado por uma maior variabilidade no uso das estratégias, por uma população que ainda não domina adequadamente o processo. Esse fato pode ser corroborado pelo achado de que apenas 50% dos indivíduos estudados é capaz de efetuar a operação soma sem uma manipulação ostensiva, e que muitos deles utilizaram manipulações discretas em alguns cálculos.
A dependência do cálculo mental a um processamento por blocos tende a tornar o tempo de processo aritmético da soma mais constante e pode explicar os resultados discordantes na literatura, que levam pesquisadores tais como Fayol, 1996, Dehaene, 1997, Dehaene et al, 1998, 1999, a sugerirem que os fatos aritméticos são memorizados com o auxílio da linguagem.
O processamento neural da subtração poderá ser compreendido levando-se em conta que a escolha da estratégica contagem regressiva e contagem crescente é dependente de uma avaliação da magnitude do possível resultado. Isso se deve ao fato de que a contagem progressiva será escolhida se o possível resultado for menor que o subtraendo ( 7 - 5 = 2 contagem 6, 7), caso contrário a contagem regressiva deverá ser utilizada ( 7 - 2 = 5 contagem 6, 5 ). Isso pode parecer inicialmente um contra senso, uma vez que para escolher a estratégia de solução deve-se antecipadamente conhecer essa mesma solução (Fayol, 1996). O conflito se resolve, lembrando-se dos circuitos de comparação numérica como aqueles ilustrados na figura 7. A avaliação da distância entre os operandos poderá ser obtida com os quantificadores QPs desde que a detecção do máximo e mínimo definida pelos quantificadores QSs entre os operandos possa determinar a ação sináptica inibidora do acumulador associado ao menor deles sobre a ação sináptica do acumulador associado ao maior dos operando sobre os processadores QPs.
Os resultados de cronometria do presente trabalho confirmam a estratégia acima como a predominante na solução da subtração, além disso, paradoxalmente, o tempo de resposta decresce com o tamanho dos operadores (Fig. 3). Isso poderá ser explicado, se o tempo gasto no processo de comparação for mais importante na determinação do tempo de resposta, pois é sabido que o tempo para decisão sobre qual o maior ou menor de dois números, é inversamente proporcional à distancia entre eles. Isto é, decresce quando um dos números aumentar em relação ao outro (Fayol, 1996; Hinrichs et al, 1981; Dehaene, 1997). Deve-se ressaltar que na determinação do tempo de resposta poder-se-ia ter dois componentes antagônicos, a comparação - cujo tempo de solução decresce com o aumentar de um dos números, e o contar - cujo tempo de solução pode crescer com o tamanho dos operandos. Esse antagonismo poderia explicar o baixo valor do coeficiente de correlação na Fig. 3, quando comparado com os relatados na literatura (Butterworth, 1999; Dehane, 1997; Fayol, 1996), pois no caso da subtração as crianças utilizaram muito menos as manipulações ostensivas e discretas. Além disso, o tempo médio de solução foi menor do que aquele obtido para a soma.
Finalmente, os resultados com o produto podem ser explicados a partir do uso de um processo de contar por bloco, que torna o processo mais rápido, pois um dos operandos seria usado como bloco pelo identificador I (Fig. 6), de modo que esse valor seria acumulado em A a cada passo definido pelo controlador C. O número de passos do processo seria determinado por um dos operandos. Num processo de otimização, o maior operando seria utilizado para gerar o bloco e o menor deles para alimentar o controlador C. Nesse caso, o tempo de resposta dependeria do mínimo entre os operandos. A regressão obtida no presente trabalho para essa hipótese atingiu uma significância estatística em torno de 10%. Um processo aleatório de distribuição dos operando sobre I e C levaria a uma dependência do tempo de resposta ao tamanho dos operando, como mostrado na Fig. 3. O uso de estratégias distintas explicaria os baixos coeficientes de correlação encontrados, pois o produto foi a operação que foi solucionada com o menor tempo médio e sem manipulação ostensiva ou discreta.
Pode-se concluir a partir da discussão acima, que o cálculo aritmético é um processo neural complexo, que envolve várias etapas (Fig. 9):
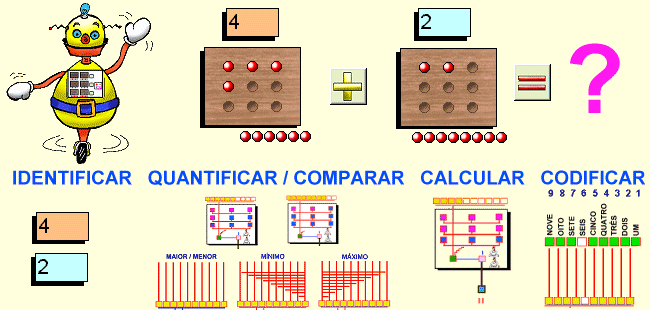
Fig. 9 O processo otimizado de cálculo
Os processos de quantificação e comparação podem ser efetuados em paralelo, por circuitos alimentados pelo mesmo acumulador, conforme representado na Fig. 8. Esse processamento paralelo é fundamental para reduzir o tempo total de solução do cálculo a realizar. Os processos de comparação e classificação são fundamentais para as estratégias de otimização dos cálculos, pois permite a utilização da regra do mínimo no caso da soma; a otimização do produto, e a escolha entre a contagem regressiva e progressiva no caso da subtração.
As diferentes etapas acima descritas são suportadas por circuitos neurais distintos, o que torna o processamento aritmético uma atividade de inúmeras áreas cerebrais, que se envolvem diferentemente na solução de cada um dos tipos de cálculo, de acordo com as diferentes estratégias utilizadas e com o objetivo de fornecer resultados mais ou menos precisos (Cochon, et al, 1999; Dehaene, 1997; Dehaene et al, 1998; Pesenti et al,1998, Ratickx et al, 2001; Rickard et al, 2000, Stanescu-Cosson et al, 2000).
A associação entre os circuitos neurais para aritmética e linguagem partilham apenas alguns elementos em comum, principalmente relacionados com a fase de identificação e recodificação. O processo de cálculo definido principalmente nas fases de quantificação, comparação e operação é suportado por um sistema neural específico, cujas propriedades básicas foram moldadas na evolução, pela necessidade de quantificar os objetos e eventos envolvidos nas atividades de sobrevivência. Esses fatos devem ser levados em conta quando do planejamento das atividades em sala de aula.
Referências
Ashcraft, M. H. (1991) Cognitive arithmetic: A review of data and theory , in Numerical Cognition, ed. Dehaene, S. , Blackwell, Oxford, U.K.
Butterworth, B (1999) The mathematical brain, Macmillan Publishers, London, U.K.
Cochon, E., Cohen, L., van de Moortele, Dehaene S. (1999) Differential contributions of the left and right ingerior parietal lobules to number processing. J. Cognitive Neurosci., 11:617-630
Dehaene, S. (1991) Varieties of numerical abilities, in Numerical Cognition, ed. Dehaene, S. , Blackwell, Oxford, U.K.
Dehaene, S. (1997) The number sense, Penguim Books, London, U.K.
Dehane, S, Dehanene-Lambertz, G. and Cohen, L. (1998) Abstract representations of numbers in the animal and human brain. Trends Neuroscience, 21:355-361
Dehaene, E, Spelke, E., Pinel, P. Stanescu, R and Tsvkin, S. (1999) Sources of mathematical thinking: Behavioral and brain-imaging evidence. Science, 284:970-974
Fayol, M. (1996) A criança e o número, Artes Médicas, Porto Alegre, Brasil
Fink, G. R., Marshall, J. C., Gurd, J., Weiss, P. H., Zafiris, O., Shah, J. J. and Zilles, K. (2001) Deriving numerosity and shape fron identical visual displays. Neuroimage, 13:46-55.
Foz, F.B., A. Rondó, M. P. Rebello, A. F. Rocha, A.F., P. B. Ramazzini., M. A. Cardoso, C. C. Leite ( 1999 ) Plasticidade neural e processamento de linguagem: efeitos de lesões congênitas na alocação dos circuitos neurais no hemisfério direito. IN: STERCHELE, R. Atualização em voz, linguagem, audição e motricidade oral. São Paulo: Frôntis Editorial
Gallistel and R. Gelman. (1991) Preverbal and verbal counting and computation, in Numerical Cognition, ed. Dehaene, S. , Blackwell, Oxford, U.K.
Gelman, R. and Meck, E. (1983) Preschoolers couting: principles before skells. Cognition, 13:343-359
Groen, J.G. and Parkman, J. M. (1972) A chronometric analhysis of simple addition. Psychological Rev., 79:329-343
Hinrinchs, J. V., Yurko, D.S. and Hu, J. M. (1981) Two digit number comparison: use of place information. J. Exptl. Psychology: Human Perception and Performance, 7:890-891
Jahanshahi, M., Dirnberger, G., Fuller, R and Frith, C. D. (2000) The role of the dorsolateral prefrontal cortx in randmom nuber generation: A study with Positron Emission Tomography. Neuroimage, 12:713-725
Jensen, E.M., Reese, E.P. and Reese, T.W. (1950) The subtizing and couting of visually presented fields of dots. The journal of Psychology, 30: 363-392
Kaufman, E. L., Lord, M. N., Reese, T. W. and Volkmann, J. (1949) The discrimination of visual number . American J. of Psychology, 62:498-525
McCloskey, M. (1991) Cognitive mechanisms in numerical processing: Evidence from acquired dyscalculia, in Numerical Cognition, ed. Dehaene, S. , Blackwell, Oxford, U.K.
Meck, W.H. and Church, R.M. (1983) A mode control model of couting and timing processes. J. Exptl. Pshychol. Anim. Brehav. Proc, 9:320-334
Mix, K. S. (1999) Preschoolers΄s recognition of numerical equivalence: Sequential sets. J. Exptl. Child Psychology, 74:309-332
Pesenti, M., Thioux, M., Seron, X. and De Volder, A. (2000) Neuroanatomical substrates of arabic number processing, numerical comparison and simple addition: A PET study, J. Cognitive Neurscience, 12:461-479
Ratinckx, R., Brysbaert, M and Reynvoet, B. (2001) Bilateral field interactions and hemispheric asymmetry in number comparison. Neuropyshologia, 39:335-345
Rickard, T. C., Romero, S. G., Basso, G., Wharton, C. , Flitman, S. and Grafman, J. (2000) The calculating brain: na fMRI study. Neuropsychologia, 38:325-335
Rocha, A. F. - Neural Nets: A theory for brains and machine. Lecture Notes in Artificial Intelligence, Springer-Verlag, 1992.
Rocha, A. F. ( 1997 ) ENSCER um sistema informatizado para ensino e diagnóstico de deficientes cerebrais. Processo 97/6020-9, PIPE FAPESP. www.enscer.com.br
Rocha, A. F. ( 1999 ) O cérebro: Um breve relato de sua função. EINA, Jundiaí
Rocha, A. F. e Rocha M. T. ( 2001 ) O cérebro na escola. EINA, Jundiaí.
Rocha, A. F., Foz, F. B. e Rondó, A, ( 2000 ) Cérebro, Cognição e o Aprender IN: Gonçalves, M. J.; Macedo, E. C.; Sennyey, A. L.; Capovilla, F. C. Org. Tecnologia e (Re)Habilitação Cognitiva 2000: a dinâmica clínica-teoria-pesquisa. São Paulo: Sociedade Brasileira de Neuropsicologia. Centro Universitário São Camilo. pp 203-211
Rocha, A.F, A. Serapião, Leite, C. C. e Menezes, R.X. (2001) Fisiopatologia de inteligência. Neurociências e Educação, 1; www.enscer.com.br
Stanescu-Cosson, R. Pinel, P., van de Moortele, P.F., LeBihan, D, Cohen, L. and Dehaene, S. (2000) Understanding dissociations in dyscalculiaL A bain imaging study of the impact of number size on the cerebral networks for exact and approximate calculation. Brain, 123:2240-2255
Stahian, K., Simon, T. J., Peterson, S., Patel, G. A., Hoffman, J.M. and Grafton, S. T. (1999) Neural evidence linking visual object enumeration and attention, J. Cognitive Neuroscience 11:36-51
Siegler, R.S. (1996) Emerging minds. Oxford University Press, Oxford, UIK
Wynn, K. (1998) Psychological foundations of number: numerical competence in human infants. Trends in Cognitive Sciences, 1998: 122-131
Wynn, K. (2000) Early numerical knowledge, in Childhood cognitive development, ed. Kang Lee, Blackwell, Oxford, U.K.
Agradecimemtos: Esse trabalho foi financiado em parte pelo CNPq Conselho Nacional de Pesquisas, dentro de seus Projetos Temáticos, Área de Educação. A coloboração dos pais e crianças foi inestimável e deve ser aqui registrada.